Project Home > Web Pages Home >
Modeling
a Single Blade in Maple :
In addition to
being able to model the blades of the twisted Savonius wind turbine
in Geometry Expressions, it is useful to model a single blade in the
Computer Algebra System (CAS) Maple. In fact, it is actually much
easier to create the blade using Maple's 3D plot feature; however,
there is much more limitation on what can be done with the blade. In
our Geometry Expressions model the surface of the blade is
constructed with traces. These traces are parameterized by s and t,
where s is the location vertically and t is the location horizontally
around the curve of the blade.


We have one point on our Geometry Expressions model that can be moved to
any place on the surface of the blade by varying s and t (see above). If
we calculate the symbolic coordinates of these points, we can input
them into a Maple 3D Plot and plot the surface of the blade
parametrically. The problem, of course is that our functionally
realistic model with cross-pieces has eight of these points.
Therefore, Our maple blade will model one of the eight sections, or
could model the squeeze again. We also need to reduce our equation to
having only two variables. Copying the equation from the top view
(below) will help with this, because the circles are constrained by r
and theta, while the ellipses are constrained by a, b, h, k and
theta.

Once we copy our
equation (as a maple input) and paste it into maple, we need to add a
third term before we can make the 3D plot. Since the point in the top
view was represented by X and Y coordinates, we need to add a Z. The
Z coordinate is defined by s, but not t, because the purpose of s is
to represent the proportion of the way up or down on the turbine the
points are. We will multiply s by a constant that will represent the
height of the turbine, because otherwise our turbine would only be 1
unit tall. It is easiest to set the radius at 1 and then adjust the
constant height accordingly. If this is to be only ¼ of the
blade (vertically), then it may be logical for the radius to exceed
the height, but this is best determined by eye. We then evaluate the
equation for a set value of r and a set value of theta, as well as
for X=0 if your equation had Xs in it. Theta=pi/4 is the realistic
theta value if we are constructing one section of a turbine twisted
180 degrees or pi radians (remember that Maple uses radians), but you
may want to see a bigger twist. Finally, we plot our expression in
the interval of our Geometry Expressions traces: t is from 0 to pi
and s is from 0 to 1. Our output is a drag-able three-dimensional
model of the twisted blade. This is a copy of the Maple worksheet
(with motion added to the 3d plots):
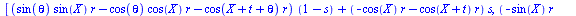
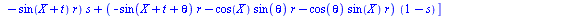 |
(1) |
| > |
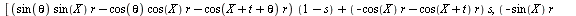
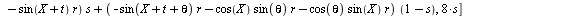 |
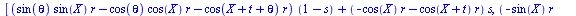
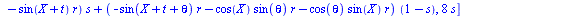 |
(2) |
| > |
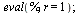 |
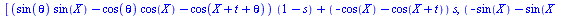
 |
(3) |
| > |
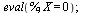 |
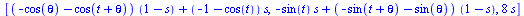 |
(4) |
| > |
 |
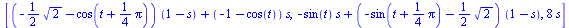 |
(5) |
| > |
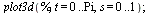 |
| > |

 |
![[`+`(`*`(sin(t), `*`(`+`(1, `-`(s)))), `*`(`+`(`-`(1), `-`(cos(t))), `*`(s))), `+`(`-`(`*`(sin(t), `*`(s))), `*`(`+`(`-`(1), `-`(cos(t))), `*`(`+`(1, `-`(s))))), `+`(`*`(8, `*`(s)))]](images%20in%20maple%20blade/Clean%20modeling%20blade%20with%20Maple_22.gif) |
(6) |
| > |
 |
Although this
method is a lot faster for modeling the blade and it makes the shape
easier to conceptualize, there are many more limitations to this
model than our Geometry Expressions one, including the inability to
change theta without re-generating the whole image, the inability to
stack multiple sections or even create the other blade, and the
inability to animate its operation. Therefore, using both methods is
useful when modeling this shape so we can take advantage of the
strengths of each one.


